クラスカル・ウォリス検定までの簡単な流れ

説明とか見ても表現が回りくどくて、言葉の意味にしろ、検定をする意味にしろ理解できない。
限りなく大雑把なまとめ。
※細かい表現や手法・目的は別サイトで調べるコト。

まずは結論

クラスカル・ウォリス検定をする理由

計算した結果

「有意差がある」、「有意差がない」

メモ・流れ

例えば、「３つの薬の中で回復値の高いモノを知りたい」
※流れを見るためなので、重複データとかは存在しない。

それぞれのデータを取得

薬を「A、B、C」とし、3つのグループにわけて調査する。
その結果が下記。

中央値なり、平均値なりで考える

中央値、平均値を出したものが下記。

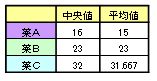
これを見る限り「薬Cの回復値が高い」となる。

このデータは偶然？

このデータを信用していいかどうかを調査する必要がある。
ひょっとしたら偶々かもしれないしね。

ということで「クラスカル・ウォリス検定」ってのが登場。

クラスカル・ウォリス検定の第一段階

まずは回復値の小さいものから「１、２、３」としていく。
番号をつけたものが下記。

クラスカル・ウォリス検定の第二段階

上記の番号の合計と項目数を数える。
※合計を「Rx」、項目数を「nx」とする。

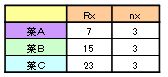
クラスカル・ウォリス検定の第三段階

「Rx」「nx」を計算式にあてはめる。
Excelでやるために…Σとか分からないし…簡単にしたモノを表記してみる。

上図にそれぞれの「Rx」や「nx」をはめ込んでいく。
「Rx」は「R1～R3」で「薬AがR1、薬BがR2、薬CがR3」とする。「nx」は「n1～n3」で同じような感じ。

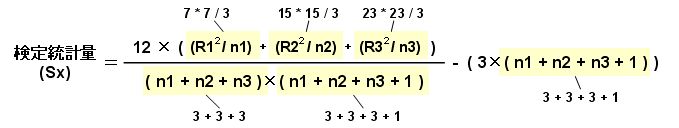
これを計算すると「検定統計量(Sx) = 5.69」となる。

クラスカル・ウォリス検定の第四段階

「カイ2乗分布の片側確率」ってヤツを求める。
コイツと前述の「有意水準」ってヤツを比較する。

「カイ2乗分布の片側確率」ってヤツはExcelで「CHIDIST()」ってヤツを使う。

「CHIDIST()」のカッコの中にいれるものは「検定統計量(Sx)」ってヤツと「グループ数から1を引いたもの」。

今回の例では「ABC」の3グループなので、Excelには「=CHIDIST(5.69,2)」をいれる。
Excelの計算によるとコレは「0.058」となる。
「0.058」をパーセント表記にすると「5.8％」。
つまり「カイ2乗分布の片側確率」は「5.8％」。

クラスカル・ウォリス検定の第五段階

「有意水準」ってヤツと比較する。
「1%」か「5%」のどっちかで比較するらしいんだけど「カイ2乗分布の片側確率」は「5.8%」なのでどっちで比較しても「有意水準」より「大きい」。

クラスカル・ウォリス検定の第六段階

「有意水準より大きい」ということなので「有意差が無い」といえる。
「有意差が無い」は「偶然の可能性が高い」ということになる。